Recent evidence shows that neural networks can quantify properties of non-linear chaotic physical systems, such as fluid turbulence, n-body problem [4], far better than the current state of the art (see e.g. [1,2,3]). This suggests that neural networks can capture certain hidden structures or symmetries better than humans. “Understanding what a machine learning model understood” is currently among the ultimate challenges with huge potential to step forward our fundamental physical understanding of these systems.
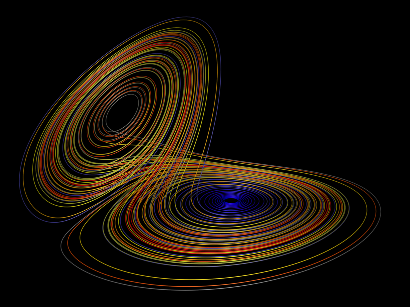
In this project, we tackle this challenge by considering possibly the simplest and most famous continuous chaotic system: the Lorenz attractor. In [1], a simple recurrent network has been proposed that is capable to recover the statistical features of the attractor. However, such network needs parameters specified by humans to work. Here, we will train end-to-end a generative model to be capable of fully reproducing physically correct signals. The model validation will be performed on this basis of the capability of the model to deliver the expected “chaoticity” (spectrum of Lyapunov exponents).
We will investigate which network architectural features make it possible to learn and reproduce chaotic features and in which aspects prevent that to happen.
Supervision: Alessandro Corbetta, Vlado Menkovski
[1] Pathak, J., Lu, Z., Hunt, B. R., Girvan, M., & Ott, E. (2017). Using machine learning to replicate chaotic attractors and calculate Lyapunov exponents from data. Chaos: An Interdisciplinary Journal of Nonlinear Science, 27(12), 121102.
[2] Ham, Y. G., Kim, J. H., & Luo, J. J. (2019). Deep learning for multi-year ENSO forecasts. Nature, 1-5.
[3] A. Corbetta, V. Menkovski, R. Benzi, F. Toschi, Deep learning velocity signals can define turbulence intensity. To be submitted.
[4] Breen, Philip G., et al. “Newton vs the machine: solving the chaotic three-body problem using deep neural networks.” arXiv preprint arXiv:1910.07291 (2019).
